Datasets

General Datasets

Suppose that the set of all choice alternatives is discrete and denoted by \(X=\{x_1,\ldots,x_m\}\).

A general dataset in this case consists of a finite collection of menus from \(X\) and the choices observed at these menus.

Datasets of this kind can be further distinguished between those with or without default/status quo options.

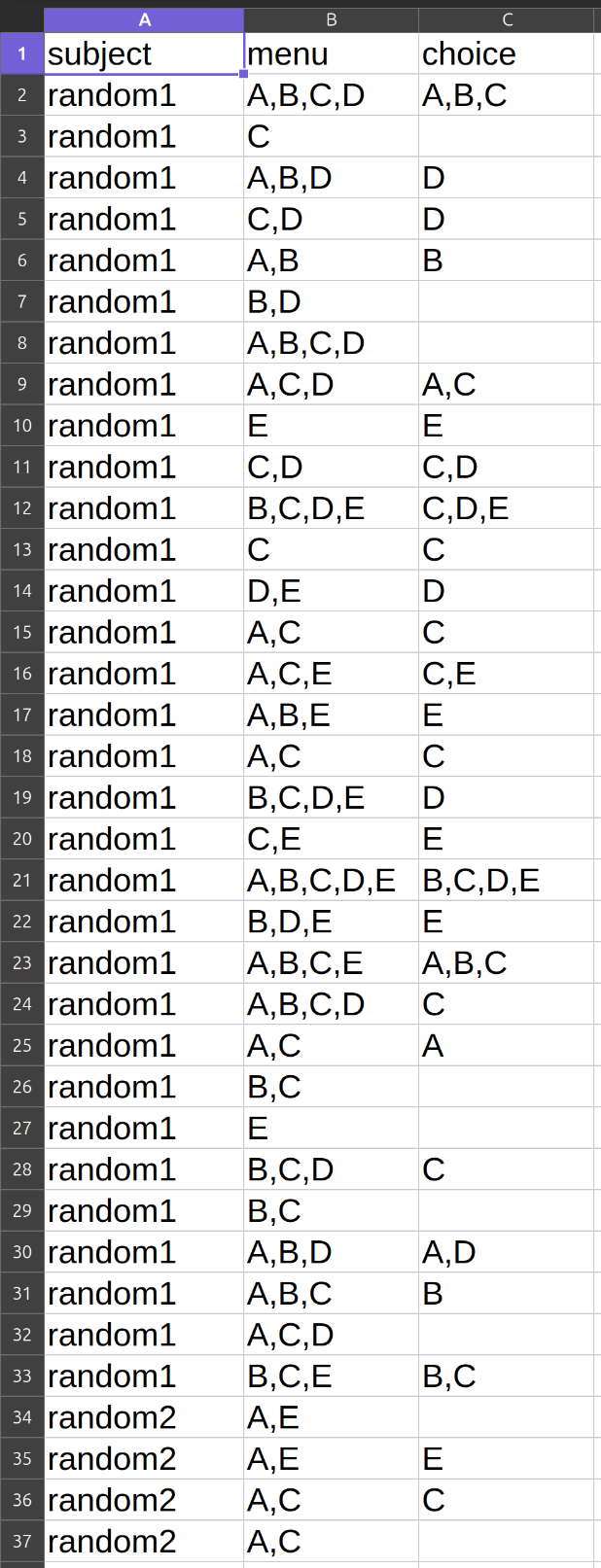
General datasets without default/status quo options

Such a dataset is a collection of \(k\) observations,

\[\mathcal{D}=\left\{\big(A_i,C(A_i)\bigr)\right\}_{i=1}^k,\]

each of them a pair that comprises a menu \(A\subseteq X\) and the alternative(s) observed to be chosen from \(A\), if any.

The choice(s) that were observed at menu \(A\) is (are) denoted by the set \(C(A)\), where \(\emptyset\subseteq C(A)\subseteq A\).

If \(C(A)\) contains more than one alternative, it is understood that the decision maker has chosen (or may be thought of as having chosen) any or all of these alternatives at \(A\), possibly over different instances where \(A\) was presented in \(\mathcal{D}\) (see also merging).

If \(C(A)=\emptyset\), it is understood that the agent has opted for the deferral outside option,

i.e. to avoid or delay making an active choice at menu \(A\).

A spreadsheet screenshot showing the structure of a general dataset without default/status quo alternatives is shown below.

The 1st column contains the subject ID; the 2nd contains the menu; and the 3rd contains the choice(s) observed at that menu.

Empty cells in the third column indicate that the subject opted for the deferral outside option at that menu.

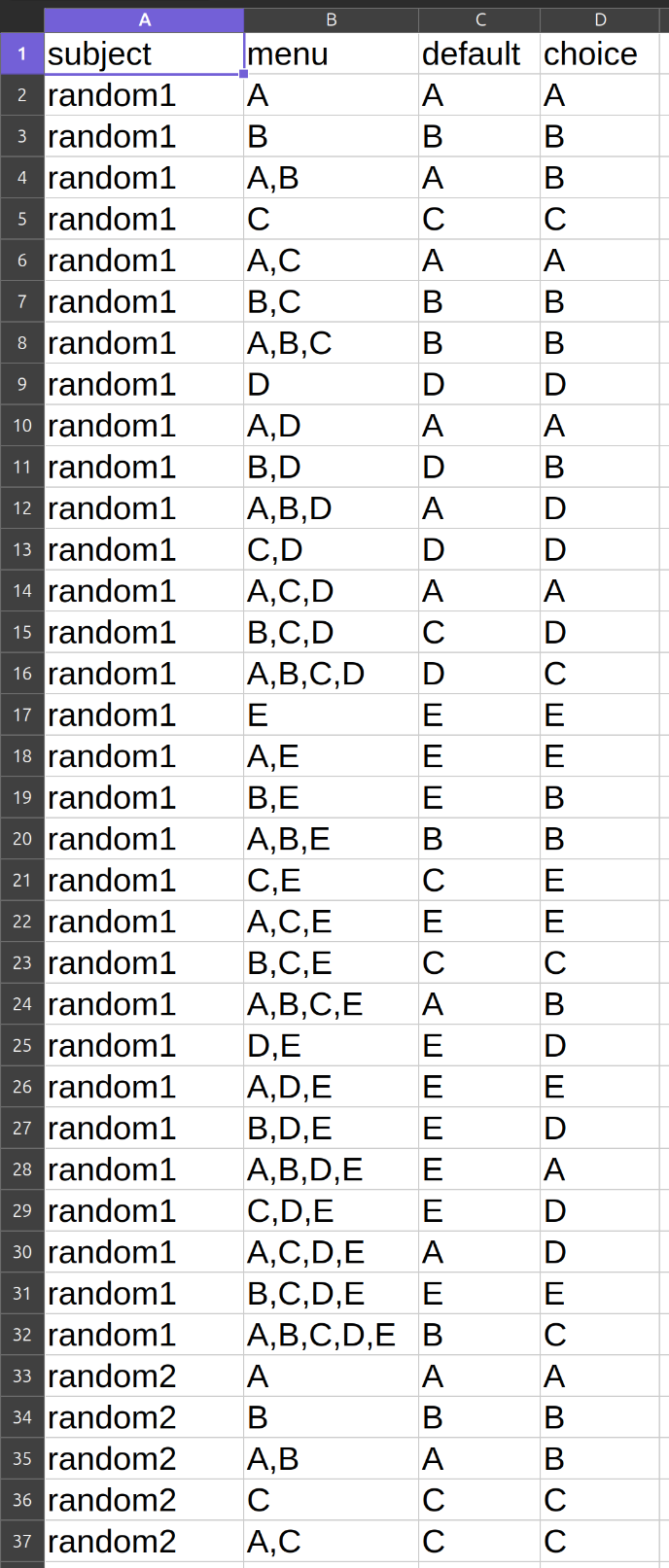
General datasets with default/status quo options

Such a dataset reflects situations where the decision makers under study are known to have been endowed with some alternative \(s\) in \(A\) before being observed to choose from menu \(A\).

Formally, a dataset of this kind is a collection of \(k\) observations,

\[\mathcal{D}=\left\{\big((A_i,s_i),C(A_i,s_i)\bigr)\right\}_{i=1}^k,\]

each of them a pair that comprises a decision problem and the alternative(s) observed to be chosen at this decision problem.

At each decision problem \((A_i,s_i)\), \(A_i\) is a menu and \(s_i\in A_i\) the default/status quo option at that menu.

Furthermore, \(\emptyset\neq C(A_i,s_i)\subseteq A_i\) is required to hold for all \(i\leq k\) in such datasets.

The interpretation of the case where \(C(A,s)\) contains more than one alternative is the same as in the case of general datasets without default/status quo options.

The reason why \(C(A,s)\) is required to be non-empty is that, at this decision problem, the individual under study is assumed to have been endowed with an observable \(s\) at \(A\) before being observed to choose from \(A\). Hence, unlike the case of general datasets without default/status quo options, not making an active choice at \((A,s)\) means choosing the alternative \(s\) in \(A\).

A spreadsheet screenshot showing the structure of a general dataset with default/status quo alternatives is shown below.

The 1st column contains the subject ID; the 2nd contains the menu; the 3rd contains the default/status quo alternative at that menu; and the 4th contains the choice(s) observed at that menu.

Tip

To be analyzable by Prest, a general dataset must be a .csv file.

An example general dataset without default/status quo alternatives.

An example general dataset with default/status quo alternatives.

An example hybrid general dataset containing both types of observations.

To import such a dataset into Prest, select “Workspace -> Import general dataset” and browse to the target file.

The new pop-up window features four column headers under “Columns”: Subject, Menu, Default and Choice.

Select the appropriate column name in your .csv file from the drop-down menu to match the corresponding column header.

If your dataset does not feature default alternatives, select “None” for the Default header.

To view the imported dataset in Prest, double-click on it in the workspace area.

Budgetary Datasets

In such datasets the analyst has observed consumer choices over bundles of \(n\) commodities and the prices of these commodities.

Prices are captured by a vector \(p=(p_1,p_2,\ldots,p_n)\in\mathbb{R}^n_{+}\), where \(p_i\geq 0\) is the price of good \(i\in\{1,\ldots,n\}\).

A consumer’s demand at these prices is captured by the consumption bundle \(x(p)\in\mathbb{R}^n_+\).

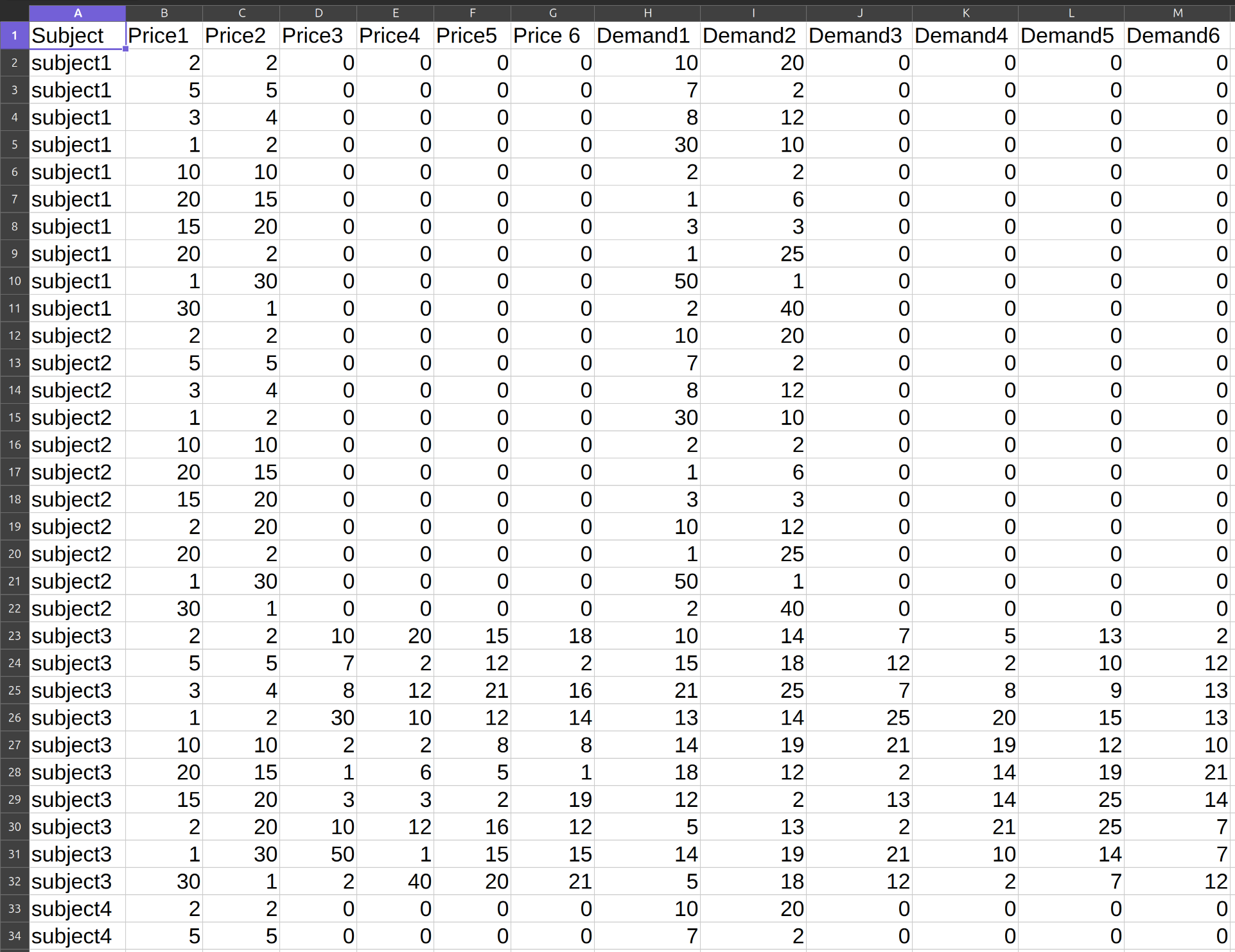
A budgetary dataset

\[\mathcal{D}=\left\{(p^i,x^i)\right\}_{i=1}^k\]

is a collection of \(k\) observations, each of them a pair \((p^i,x^i)\) comprising the consumption bundle \(x^i\) that was observed to be chosen when prices were \(p^i\).

A spreadsheet screenshot showing the structure of a budgetary dataset is shown below.

The 1st column contains the subject ID; columns 2 to 7 contain the prices of the goods; and columns 8 to 13 contain the quantities of the goods chosen by the subject at these prices.

Tip

To be analyzable by Prest, a budgetary dataset must be a .csv file.

An example budgetary dataset.

To import such a dataset, go to “Workspace -> Import budgetary dataset” and select the target file from the relevant directory.

Budgetary datasets with \(n\) goods must have the following structure:

• Column 1: subject ID

• Column 2: price of good 1

• Column \(n+1\): price of good \(n\)

• Column \(n+2\): demand of good 1

• Column \(2n+1\): demand of good \(n\)

To view the imported dataset, double-click on it in the workspace area. An extra column with the total expenditure associated with each observation is added automatically.